All points in a plane are colored using three colors. Prove that there exists a triangle with vertices having the same color such that either it is isosceles or its angles are in geometric progression.

This problem was asked in the Indian National Mathematics Olympiad 2009.

Let us consider a circle in this plane and mark 7 equidistant points on the circumference (any two adjacent points are an arc length d apart), and mark them A, B, C, D, E, F and G. By Pigeonhole Principle, we can say that there are atleast three points which have the same color.

Let us pick A as one of these three points (you can choose any, as it is symmetrical). Lets list down all the possible triangles that can be formed :

ABC ABG ACG AEF

ABD ACD ADE AEG

ABE ACE ADF AFG

ABF ACF ADG

The possible distinct triangles are denoted below :

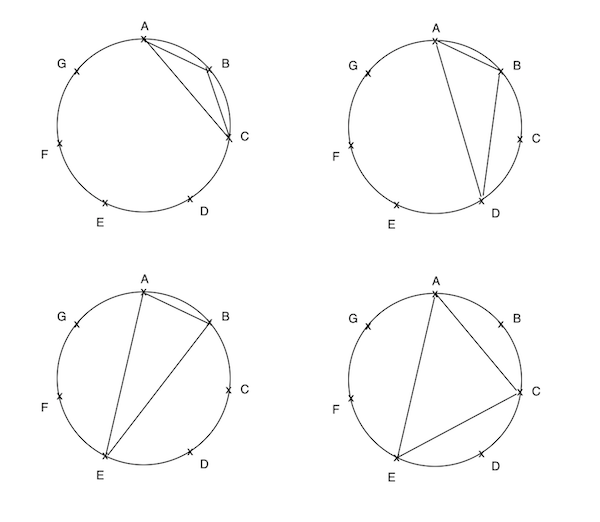
Note : the other triangles formed are just realignments of the above four triangles.

Now in the above, ABC, ABE and ACE are isosceles triangles (compare the lengths of arcs). We need to prove the angles of ABD are in geometric progression.

Consider a heptagon drawn with these 7 points as its vertices. Then each interior angle = \(\pi / 7\) . Draw line segments from D to all vertices.

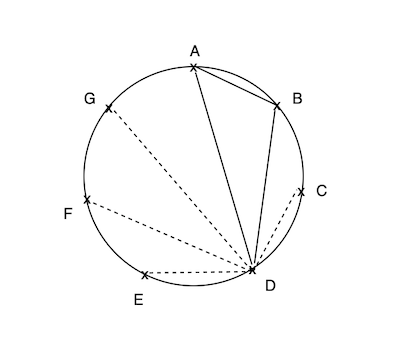
From the above, we know that

\(\angle ADB = \pi / 7\).

With the same logic, we know \(\angle DAG : \angle DAB = 3 : 2\). Since \(\angle GAB = 5\pi / 7\) , we have \(\angle DAB = 2\pi / 7\).

Sum of angles in a triangle is \(\pi\), hence \(\angle ADB + \angle DAB + \angle ABD = \pi\). Or , \(\angle ABD = 4\pi / 7\).

We can see that \(\pi / 7\), \(2\pi / 7\), and \(4\pi / 7\) are in geometric progression.

This completes the proof.